El cuadro de la izquierda en si está distorsionado por completo. Pero cuando se mira por un espejo en forma de tubo de quinqué las imágenes retornan a su forma normal. El artista, al pintar no mira directamente la realidad sino que lo hace guiado solamente por lo que se refleja en un espejo curvo.
Bernhard Riemann se ocupó de los espacios curvos. En dicho espacio se muestran las trayectorias más cortas entre puntos son líneas curvas, los triángulos se modifican al moverlos y la suma de sus ángulos interiores, en lugar de ser 180 grados, varía cuando los triángulos se trasladan.
Como consecuencia de lo anterior, la perspectiva ya no la podemos representar con estirar o contraer el plano cartesiano o espacio "plano clásico", para explicar la anamorfosis, como aconteció con la elipse y el círculo y el perro, sino que debemos recurrir a las fórmulas de Bernhard Riemann, y nuevamente se soluciona el problema de pasar de una perspectiva plana a una curva, en donde el espacio se retuerce sobre sí mismo, etc.
La figura de la derecha muestra la manera de pasar de un perspectiva curva y retorcida a una normal, ya que no debemos olvidar que las elipses, hipérbolas, parábolas y circunferencias provienen de la misma cantera.
Samuel Marolois recoge en su tratado de perspectiva de 1630 el método de Laurente publicado por Danti y lo aplica al siguiente dibujo de un perro.
Primero se ve el dibujo original cuadriculado, y después el mismo dibujo alargado en sentido horizontal en una proporción mayor de 3 a 1. Si miramos esta figura desde el lateral derecho con el ojo muy cerca del dibujo, observaremos que se produce un acortamiento de la figura en sentido horizontal y, al mismo tiempo, veremos converger hacia la izquierda las líneas horizontales de la cuadrícula. Sólo viéndola desde el infinito, se obtiene una restitución semejante a la imagen original.
Anamorfosis a través de un procedimiento matemático
Anamorfosis de un círculo en una elipse
La desfiguración de la circunferencia (con su aplastamiento distorsiona el plano cartesiano asociado a ella), se denomina anamorfosis, que corresponde a una perspectiva muy especial. El término anamorfosis se toma del griego que significa "trasformar".
En el caso del círculo, el plano cartesiano está compuesto por varios cuadraditos, en cambio, cuando el círculo se aplasta –transformándolo en una elipse– esos cuadrados se deforman quedando más contraídos por el eje Y, y dilatados simultáneamente por el eje X, según se visualiza en la imagen.
- Ejemplo
Utilizando las propiedades que tiene el «semieje mayor» y, a la vez, la relación de afinidad con la Circunferencia principal, o la Excentricidad, o la Contracción de Lorentz, constataremos que para el ejemplo y los valores dados, podemos determinar el factor asociado al ángulo  y, a la vez, el factor del ángulo
y, a la vez, el factor del ángulo  , tendremos:
, tendremos:
 y, a la vez, el factor del ángulo
y, a la vez, el factor del ángulo  , tendremos:
, tendremos:
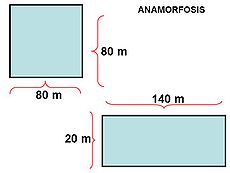
Si el radio "Y" del círculo es de 80 m y éste se contrajo a 20 m, dado que (80 - 60), y el radio "X" de 80 m se dilató en 140 m, dado que (80 + 60), entonces en la elipse su «semieje mayor» será de 100 m, y su «semieje menor» de 60 m, por cuanto los valores alteradores son 80 y 60, por lo que el 

El trazo 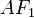 será de 20 m, y el trazo
será de 20 m, y el trazo  , será de 80.
, será de 80.
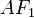 será de 20 m, y el trazo
será de 20 m, y el trazo  , será de 80.
, será de 80.- Si dividimos 20/80 = 0,25 igual al factor de contracción del eje de las Y, en donde 80 x 0, 25 = 20 = (80- 60)
- Si dividimos 140/80 = 1,75 igual al factor de dilatación del eje de las X, en donde 80 x 1,75 = 140 = (80 + 60)
-
- Dado que

- Dado que
- Los valores involucrados en este ejemplo son:
Anamorfosis de un esfera en un plano
Otro ejemplo matemático de anamorfosis lo encontramos en la proyección estereográfica, que consiste en aplastar una esfera hasta convertirlo en un plano, en donde la idea es proyectar cada punto de la esfera sobre un plano.
Algunos ejemplos de artistas urbanos
Julian Beever es artista británico especializado en anamorfosis que plasma en sus obras, generalmente murales de tiza en las aceras de las calles de distintas ciudades.
Eduardo R. Relero es un artista argentino de Rosario que reside en España, donde realiza en el suelo de distintas ciudades dibujos anamorficos con temas satíricos o de crítica social.









![\,S^2\,\,=\,\,[\,x^2\,\,+\,\,y^2\,\,+\,\,z^2\,\,]\, =\,\,1](http://upload.wikimedia.org/math/8/8/4/8844d35afa7fd11ea1186517893f3124.png)
No hay comentarios:
Publicar un comentario